If you’ve ever seen a picture of a DNA molecule, you probably saw it in its famous B-form: two strands coiling around each other in a right-handed fashion to form a double helix. But did you know that DNA can change its shape?

DNA molecules, which carry the genetic code of an organism, have to be tightly packed to fit inside a cell. However, every few hours, the cell produces a faithful copy of its genome in preparation for cell division. This replication process puts tremendous stress on the DNA and can change its shape in lethal ways.

As a mathematician and a biologist, I am interested in how mathematics can describe the many shapes of DNA, as well as cellular processes like DNA replication. The answers to these questions inspire new mathematics and possibly a better understanding of the molecule of life.

The shape of DNA

To understand the mathematics of the shape of DNA, you need to consider both its geometry and its topology. These are related but distinct concepts.

Geometry describes an object at a particular moment in time – frozen rigid in space, like a sculpture. In the cell, the DNA helix coils upon itself, or “supercoils.” The way DNA folds and coils encodes valuable geometric information that can be crucial to control the way genes are expressed.

Topology describes how an object deforms smoothly, as if made out of clay without making new holes or breaks. For example, imagine a rubber band tumbling around in a whirlpool. As the water swirls, the rubber band twists, stretches and shrinks. All of the shapes adopted by the band as it moves are topologically identical, but geometrically different.

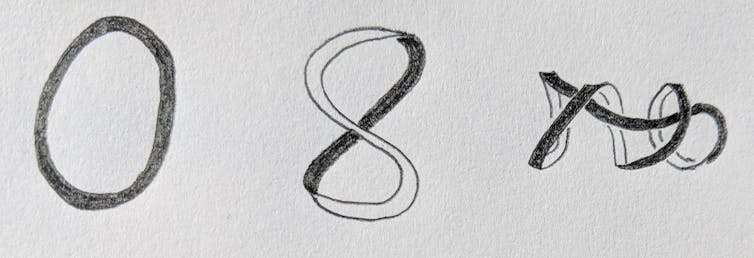
Merely copying DNA creates a large number of shape-related problems, but textbook images rarely illustrate this topological conundrum.

During the cell cycle, each chromosome is replicated into two identical copies. In order for that to happen, the DNA helix must unwind, causing stress on the DNA. DNA responds to this stress by supercoiling, just like an old telephone cord. But the cell cannot tolerate too much supercoiling. If DNA contorts too much, the cell will suffer.

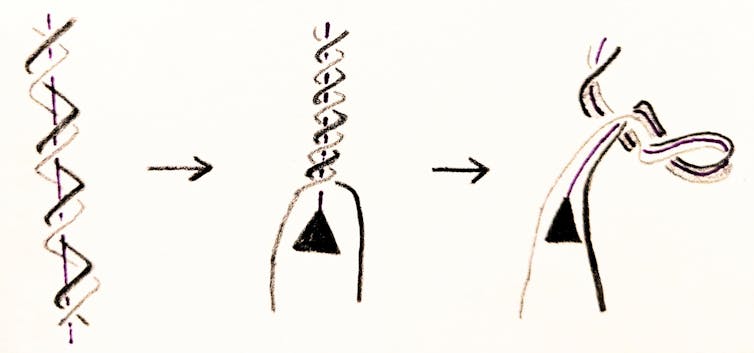
A DNA molecule can be linear – as in the case of human chromosomes – or circular. Examples of circular DNA molecules include bacterial chromosomes and human mitochondrial DNA. If the DNA molecule is circular, then cellular processes such as replication may tie DNA into knots or links, like rings in a keychain. DNA knots and links can cause cells to malfunction or even die.

Stabilizing DNA

Consider the bacterium E. coli. Its genetic code is found in one single DNA chromosome. In E. coli and other bacteria, the DNA double helix closes into a circle, like a twisted rubber band.

Replication of the E. coli chromosome can happen in as short as 20 minutes in a test tube. But when a circular chromosome is replicated, the process yields two interlinked chromosomes. That is, the new chromosomes form two rings linked through each other. The new chromosomes must unlink before the cell divides into two cells. Otherwise they would either break on the way to their target cell, or one cell would inherit two interlinked copies of one chromosome and the other one would be missing the chromosome altogether.

The cell recruits enzymes to unlink the DNA. Enzymes called topoisomerases and recombinases act as scissors and glue for DNA. They can change the geometry and topology of DNA, thus maintaining a stable genome. In E. coli, topoisomerases work tirelessly during and after replication to maintain healthy levels of supercoiling and to safely unlink the chromosomes.

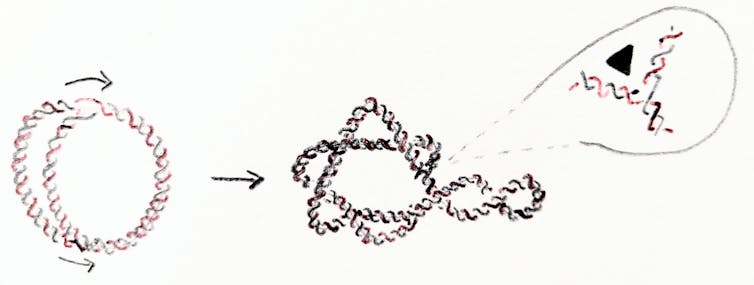
When topoisomerases don’t work

When topoisomerases don’t work, the cell eventually dies. This makes them good targets for drug design. But cells have different types of topoisomerases and other enzymes such as recombinases that may be able to come to the rescue. For example, we showed that, in E. coli cells where the topoisomerases in charge of unlinking have been disabled, other enzymes called site-specific recombinases can untie replication links.

Both topoisomerases and site-specific recombinases bind double stranded DNA and can change its shape by introducing breaks. Type II topoisomerases introduce a break along the DNA molecule and transport another piece of DNA through the break before resealing it. Site-specific recombinases attach to two sites along the DNA, introduce one cut in each, then reconnect the ends.

My lab uses mathematics and computer simulations to understand how these enzymes unlink DNA molecules. While the local action is well understood on a biochemical level, how exactly enzymes simplify the topology of DNA is still a mystery.

In one of our studies, we focused on E. coli cells where the topoisomerases don’t work. We showed how to untie a replication link in the minimum number of steps.

In general, there can be many unlinking pathways. We use computer simulations to assign probabilities to each pathway. Our work indicates that, in the case of replication links, the simplest pathway is the one that enzymes most likely take.

Sophisticated mathematical methods can help explain how enzymes unlink DNA. Without mathematical modeling, researchers would be restricted to simplified models suggested by biological experiments.

Mariel Vazquez receives funding from the National Science Foundation (CAREER DMS 1519375, DMS 1716987 and DMS 1817156).