Probability underpins AI, cryptography and statistics. However, as the philosopher Bertrand Russell said, “Probability is the most important concept in modern science, especially as nobody has the slightest notion what it means.”

I teach statistics to engineers, so I know that while probability is important, it is counterintuitive.

Probability is a branch of mathematics that describes randomness. When scientists describe randomness, they’re describing chance events – like a coin flip – not strange occurrences, like a person dressed as a zebra. While scientists do not have a way to predict strange occurrences, probability does predict long-run behavior – that is, the trends that emerge from many repeated events.

Modeling with probability

Since probability is about events, a scientist must choose which events to study. This choice defines the sample space. When flipping a coin, for example, you might define your event as the way it lands.

Coins almost always land on heads or tails. However, it’s possible – if very unlikely – for a coin to land on its side. So to create a sample space, you’d have two choices: heads and tails, or heads, tails and side. For now, ignore the side landings and use heads and tails as our sample space.

Next, you would assign probabilities to the events. Probability describes the rate of occurrence of an event and takes values between 0% and 100%. For example, a fair flip will tend to land 50% heads up and 50% tails up.

To assign probabilities, however, you need to think carefully about the scenario. What if the person flipping the coin is a cheater? There’s a sneaky technique to “wobble” the coin without flipping, controlling the outcome. Even if you can prevent cheating, real coin flips are slightly more probable to land on their starting face – so if you start the flip with the coin heads up, it’s very slightly more likely to land heads up.

In both the cheating and real flip cases, you need an appropriate sample space: starting face and other face. To have a fair flip in the real world, you’d need an additional step where you randomly – with equal probability – choose the starting face, then flip the coin.

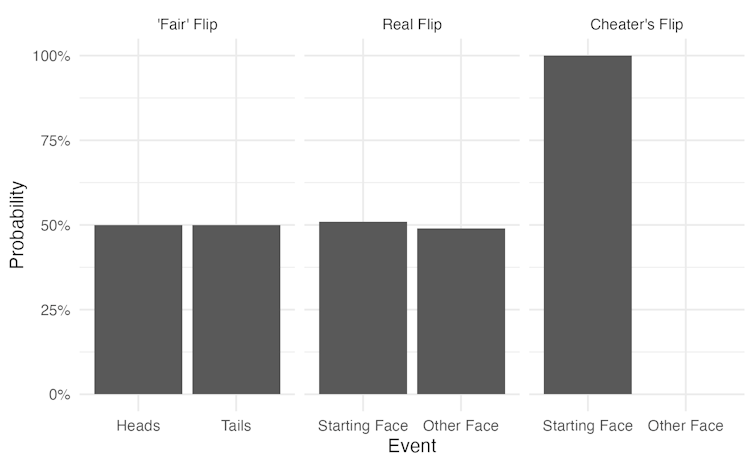
These assumptions add up quickly. To have a fair flip, you had to ignore side landings, assume no one is cheating, and assume the starting face is evenly random. Together, these assumptions constitute a model for the coin flip with random outcomes. Probability tells us about the long-run behavior of a random model. In the case of the coin model, probability describes how many coins land on heads out of many flips.

But instead of using a random model, why not just solve the coin toss using physics? Actually, scientists have done just that, and the physics shows that slight changes in the speed of the flip determine whether it comes up heads or tails. This sensitivity makes a coin flip unpredictable, so a random model is a good one.

Frequency vs. probability

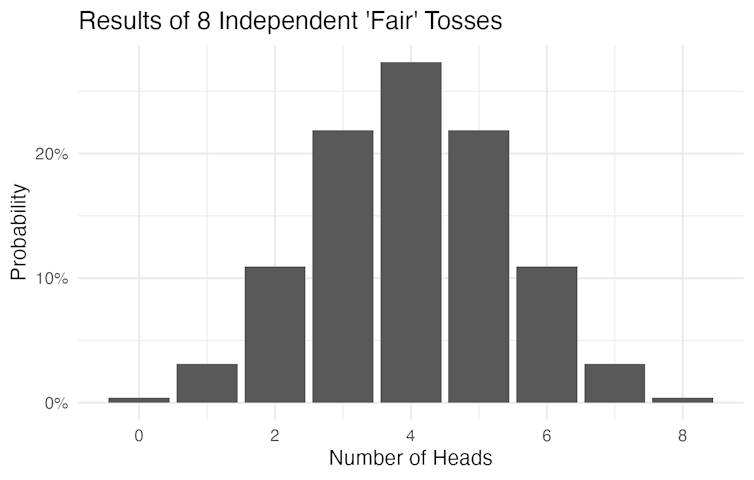
Probability differs from frequency, which is the rate of events in a sequence. For example, if you flip a coin eight times and get two heads, that’s a frequency of 25%. Even if the probability of flipping a coin and seeing heads is 50% over the long run, each short sequence of flips will come out different. Four heads and four tails is the most probable outcome from eight flips, but other events can – and will – happen.

Frequency and probability are the same in one special setting: when the number of data points goes to infinity. In this sense, probability tells us about long-run behavior.

Applications to AI, cryptography and statistics

Probability isn’t just useful for predicting coin flips. It underlies many modern technological systems.

For example, AI systems such as large language models, or LLMs, are based on next-word prediction. Essentially, they compute a probability for the words that follow your prompt. For example, with the prompt “New York” you might get “City” or “State” as the predicted next word, because in the training data those are the words that most frequently follow.

But since probability describes randomness, the outputs of a LLM are random. Just like a sequence of coin flips is not guaranteed to come out the same way every time, if you ask an LLM the same question again, you will tend to get a different response. Effectively, each next word is treated like a new coin flip.

Randomness is also key to cryptography: the science of securing information. Cryptographic communication uses a shared secret, such as a password, to secure information. However, surprising randomness isn’t good enough for security, which is why picking a surprising word is a bad choice of password. A shared secret is only secure if it’s hard to guess. Even if a word is surprising, real words are easier to guess than flipping a “coin” for each letter.

You can make a much stronger password by using probability to choose characters at random on your keyboard – or better yet, use a password manager.

Finally, randomness is key in statistics. Statisticians are responsible for designing and analyzing studies to make use of limited data. This practice is especially important when studying medical treatments, because every data point represents a person’s life.

The gold standard is a randomized controlled trial. Participants are assigned to receive the new treatment or the current standard of care based on a fair coin flip. It may seem strange to do this assignment randomly – using coin flips to make decisions about lives. However, the unpredictability serves an important role, as it ensures that nothing about the person affects their chance to get the treatment: not age, gender, race, income or any other factor. The unpredictability helps scientists ensure that only the treatment causes the observed result and not any other factor.

So what does probability mean? Like any kind of math, it’s only a model, meaning it can’t perfectly describe the world. In the examples discussed, probability is useful for describing long-term behaviors and using unpredictability to solve practical problems.

Zachary del Rosario has received funding from the National Science Foundation and Toyota Research Institute.